Zwei Senkrechte zu einer Ebene. Vorlesung über Mathematik zum Thema „Zeichen der Rechtwinkligkeit zweier Ebenen“. Thema: Rechtwinkligkeit von Linien und Ebenen

Zwei Ebenen, die sich schneiden, werden aufgerufen aufrecht, wenn die dritte Ebene senkrecht zur Schnittlinie dieser beiden Ebenen diese entlang senkrechter Linien schneidet (siehe Abbildung).

Jede Ebene senkrecht zur Schnittlinie senkrechter Ebenen schneidet diese entlang senkrechter Linien.

Zeichen der Rechtwinkligkeit von Ebenen

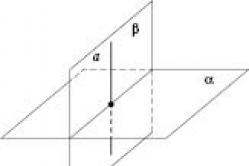
Satz 1. Wenn eine Ebene durch eine Linie verläuft, die senkrecht zu einer anderen Ebene steht, dann stehen diese Ebenen senkrecht (siehe Abbildung).

Satz 2. Wenn eine Linie, die in einer von zwei senkrechten Ebenen liegt, senkrecht zur Schnittlinie steht, dann steht sie auch senkrecht zur zweiten Ebene (siehe Abbildung).

Beispiel für die Anwendung von Satz 2
Es seien zwei senkrecht zueinander stehende Ebenen vorhanden, die sich in einer geraden Linie schneiden A(siehe Bild). Finden Sie die Entfernung von einem Punkt A, das in der Ebene liegt und nicht in der Ebene liegt, die Ebene.

In der Ebene konstruieren wir eine Senkrechte zu A durch den Punkt A. Lass ihn überqueren A am Punkt B. AB- der erforderliche Abstand.
Achten Sie darauf.
1. Durch einen Punkt außerhalb der Ebene können viele Ebenen senkrecht zu dieser Ebene gezeichnet werden (siehe Abbildung). (Aber sie verlaufen alle durch eine gerade Linie senkrecht zu dieser Ebene, die durch einen bestimmten Punkt verläuft.)

2. Wenn eine Ebene senkrecht zu einer bestimmten Ebene steht, bedeutet dies nicht, dass sie senkrecht zu einer beliebigen Geraden parallel zu dieser Ebene steht.
Zum Beispiel in der Abbildung unten und schneiden sie sich in einer geraden Linie B, Und A betritt eines der Flugzeuge und . Daher gerade A gleichzeitig parallel zu zwei senkrechten Ebenen.

Rechtwinkligkeit von Ebenen Definition. Zwei Ebenen heißen senkrecht, wenn der lineare Winkel am Rand des Diederwinkels zwischen diesen Ebenen eine Gerade ist.
Zeichen Rechtwinkligkeit von Ebenen. Wenn eine Ebene durch eine Gerade geht, die senkrecht zu einer anderen Ebene steht, dann stehen diese Ebenen senkrecht zueinander.
Nachweisen. Lassen A Und ? - zwei sich schneidende Ebenen, Mit- die Linie ihres Schnittpunkts und A- gerade senkrecht zur Ebene? und im Flugzeug liegenA. A - Schnittpunkt der LinienA Und Mit. In einem Flugzeug? vom Punkt Und wir werden wiederherstellen senkrecht, und lass es eine gerade Linie sein. B A Gerade aufrecht senkrecht, und lass es eine gerade Linie sein Flugzeuge? , was bedeutet, dass es senkrecht zu jeder Geraden in dieser Ebene ist, also zu Geraden MitUnd . aufrecht A Winkel zwischen Geraden Und B - A lineare Ebenen Und ? und es ist gleich 90°, also Wie A geradesenkrecht, und lass es eine gerade Linie seinsenkrecht zu einer GeradenA(bewiesen). Durch die Definition einer Ebene Und ?

aufrecht.. Satz 1 Wenn wir von einem Punkt aus zeichnen, der zu einer von zwei senkrechten Ebenen gehört
senkrecht zu einer anderen Ebene, dann liegt diese Senkrechte vollständig in der ersten Ebene. A Nachweisen. Lassen Und ? - senkrechte Ebenen und Mit - die gerade Linie ihres Schnittpunkts, A - Punkt A flach liegen Mit. und nicht direkt dazugehörend A Senkrecht zur Ebene? vom Punkt A gezeichnet liegt nicht in der Ebene , dann ist Punkt C die Basis diese Senkrechte liegt in Mit. Flugzeug? und gehört nicht zur Linie Mit. Von Punkt A senken wir die Senkrechte ABdirektDie Linie AB ist senkrechtEbene (ich verwende Satz 2). Durch die Gerade AB und Punkt C ? Sollen wir ein Flugzeug zeichnen? (Eine Gerade und ein Punkt definieren eine Ebene, und zwar nur eine). Wir sehen das darin Flugzeug A.

Von einem Punkt A zur Geraden BC werden zwei Senkrechte gezogen, was nicht passieren kann, also die Gerade AC. fällt mit der Geraden AB zusammen und die Gerade AB liegt wiederum vollständig in der EbeneSatz 2
Nachweisen. Lassen A Wenn wir in einer von zwei senkrechten Ebenen eine Senkrechte zu ihrer Linie zeichnen Und ? - senkrechte Ebenen und Schnittpunkt, dann ist diese Senkrechte senkrecht zur zweiten Ebene. Und ? - zwei senkrechte Ebenen, die Linie ihres Schnittpunkts und A - Mit und im Flugzeug liegenAgerade A Winkel zwischen Geraden Mit. senkrecht zu einer Geraden. A - Schnittpunkt der Linien Im Flugzeug? Von Punkt A aus stellen wir die Senkrechte wieder her und lassen sie eine gerade Linie sein A Flugzeuge? , was bedeutet, dass es senkrecht zu jeder Geraden in dieser Ebene ist, also zu Geradensenkrecht, und lass es eine gerade Linie sein B. Winkel zwischen Geraden- linear A Winkel am Rand des Diederwinkels dazwischen FlugzeugeA Und ? und es ist gleich 90°, da die Ebene A Und ?senkrecht, und lass es eine gerade Linie seinaufrecht. Gerade Mit senkrecht zu einer Geraden(nach bewiesen) und direkt A nach Bedingung.

Es ist also gerade

Yandex.RTB R-A-339285-1

Wenn es einen Winkel zwischen sich schneidenden Linien gibt, können wir über die Definition senkrechter Ebenen sprechen.

Definition 1

Vorausgesetzt, dass der Winkel zwischen senkrechten Linien 90 Grad beträgt, werden sie aufgerufen aufrecht.

Die Bezeichnung der Rechtwinkligkeit wird üblicherweise mit dem Zeichen „⊥“ geschrieben. Wenn die Bedingung besagt, dass die Ebenen α und β senkrecht zueinander stehen, dann hat der Eintrag die Form α ⊥ β. Das Bild unten zeigt es im Detail.

Wenn im Fang angegeben ist, dass die Ebenen α und β senkrecht stehen, bedeutet dies, dass α senkrecht zu β steht und umgekehrt. Solche Ebenen heißen zueinander senkrecht. Beispielsweise stehen Wand und Decke in einem Raum senkrecht zueinander, da sie beim Schnittpunkt einen rechten Winkel bilden.

Rechtwinkligkeit von Ebenen – Zeichen und Bedingung der Rechtwinkligkeit

In der Praxis kann es zu Aufgaben kommen, bei denen es darum geht, die Rechtwinkligkeit bestimmter Ebenen zu bestimmen. Zuerst müssen Sie den Winkel zwischen ihnen bestimmen. Wenn es 90 Grad beträgt, gelten sie gemäß der Definition als senkrecht.

Um die Rechtwinkligkeit zweier Ebenen zu beweisen, wird das Zeichen der Rechtwinkligkeit zweier Ebenen verwendet. Die Formulierung enthält die Konzepte einer senkrechten Linie und einer Ebene. Schreiben wir die genaue Definition des Rechtwinkligkeitskriteriums in Form eines Theorems.

Satz 1

Wenn eine von zwei gegebenen Ebenen eine Gerade senkrecht zur anderen Ebene schneidet, dann stehen die gegebenen Ebenen senkrecht zueinander.

Der Beweis ist im Geometrielehrbuch für die Klassen 10-11 verfügbar, wo es eine ausführliche Beschreibung gibt. Aus dem Vorzeichen folgt: Wenn eine Ebene senkrecht zur Schnittlinie zweier gegebener Ebenen steht, dann steht sie auch senkrecht zu jeder dieser Ebenen.

Es gibt eine notwendige und hinreichende Beweisvoraussetzung. Betrachten wir sie für die Rechtwinkligkeit zweier gegebener Ebenen, die zur Überprüfung ihrer Rechtwinkligkeit verwendet werden und sich in einem rechtwinkligen Koordinatensystem des dreidimensionalen Raums befinden. Damit der Beweis gültig ist, muss die Definition des Normalenvektors einer Ebene angewendet werden, die dabei hilft, die notwendige und ausreichende Bedingung für die Rechtwinkligkeit von Ebenen zu beweisen.

Satz 2

Damit die Rechtwinkligkeit sich schneidender Ebenen offensichtlich ist, ist es notwendig und ausreichend, dass sich die Normalenvektoren der gegebenen Ebenen im rechten Winkel schneiden.

Nachweisen

Es sei ein rechteckiges Koordinatensystem im dreidimensionalen Raum angegeben. Wenn wir n 1 → = (A 1, B 1, C 1) und n 2 → = (A 2, B 2, C 2) haben, die Normalvektoren der gegebenen Ebenen α und β sind, dann ist a notwendig und ausreichend Bedingung für die Rechtwinkligkeit der Vektoren n 1 → und n 2 → wird die Form annehmen

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Von hier aus erhalten wir, dass n 1 → = (A 1, B 1, C 1) und n 2 → = (A 2, B 2, C 2) Normalenvektoren gegebener Ebenen sind und für die Realität der Rechtwinkligkeit von α und β es ist notwendig und ausreichend, damit das Skalarprodukt der Vektoren n 1 → und n 2 → gleich Null ist und daher die Form annimmt n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .

Die Gleichheit ist erfüllt.

Schauen wir uns Beispiele genauer an.

Beispiel 1

Bestimmen Sie die Rechtwinkligkeit der im rechteckigen Koordinatensystem O x y z angegebenen Ebenen des dreidimensionalen Raums, der durch die Gleichungen x - 3 y - 4 = 0 und x 2 3 + y - 2 + z 4 5 = 1 angegeben ist?

Lösung

Um die Antwort auf die Frage der Rechtwinkligkeit zu finden, müssen Sie zunächst die Koordinaten der Normalenvektoren der gegebenen Ebenen ermitteln und anschließend die Rechtwinkligkeit prüfen.

x - 3 y - 4 = 0 ist eine allgemeine Gleichung der Ebene, aus der Sie sofort die Koordinaten des Normalenvektors gleich n 1 → = (1, - 3, 0) umwandeln können.

Um die Koordinate des Normalenvektors der Ebene x 2 3 + y - 2 + z 4 5 = 1 zu bestimmen, gehen wir von der Gleichung der Ebene in Segmenten zur allgemeinen Gleichung über.

Dann erhalten wir:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

Dann sind n 2 → = 3 2, - 1 2, 5 4 die Koordinaten des Normalenvektors der Ebene x 2 3 + y - 2 + z 4 5 = 1.

Fahren wir mit der Berechnung des Skalarprodukts der Vektoren n 1 → = (1, - 3, 0) und n 2 → = 3 2, - 1 2, 5 4 fort.

Wir erhalten, dass n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

Wir sehen, dass es ungleich Null ist, was bedeutet, dass die gegebenen Vektoren nicht senkrecht sind. Daraus folgt, dass die Ebenen auch nicht senkrecht sind. Die Bedingung ist nicht erfüllt.

Antwort: Ebenen stehen nicht senkrecht.

Beispiel 2

Das rechteckige Koordinatensystem O x y z hat vier Punkte mit den Koordinaten A - 15 4, - 7 8, 1, B 17 8, 5 16, 0, C 0, 0, 3 7, D - 1, 0, 0. Prüfen Sie, ob die Ebenen A B C und A B D senkrecht zueinander stehen.

Lösung

Zuerst müssen Sie das Skalarprodukt der Vektoren dieser Ebenen berechnen. Wenn es gleich Null ist, können wir nur in diesem Fall davon ausgehen, dass sie senkrecht sind. Wir finden die Koordinaten der Normalenvektoren n 1 → und n 2 → Ebenen A B C und A B D.

Aus den gegebenen Koordinaten der Punkte berechnen wir die Koordinaten der Vektoren A B → , A C → , A D → . Wir bekommen das:

A B → = 47 8, 19 16, - 1, A C → = 15 4, 7 8, - 4 7, A D → = 11 4, 7 8, - 1.

Der Normalenvektor der Ebene A B C ist das Vektorprodukt der Vektoren A B → und A C → und für A B D das Vektorprodukt von A B → und A D →. Von hier aus verstehen wir das

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 i → - 11 28 j → + 11 16 k → ⇔ n 1 → = 11 56 , - 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 i → + 25 8 j → + 15 8 k → ⇔ n 2 → = - 5 16 , 25 8 , 15 8

Beginnen wir mit der Suche nach dem Skalarprodukt n 1 → = 11 56, - ​​​​11 28, 11 16 und n 2 → = - 5 16, 25 8, 15 8.

Wir erhalten: n 1 → , n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Wenn es gleich Null ist, dann sind die Vektoren der Ebenen A B C und A B D senkrecht, dann sind die Ebenen selbst senkrecht.

Antwort: Ebenen sind senkrecht.

Es war möglich, die Lösung anders anzugehen und die Gleichungen der Ebenen A B C und A B D zu verwenden. Nachdem die Koordinaten der Normalenvektoren dieser Ebenen ermittelt wurden, könnte überprüft werden, ob die Bedingung der Rechtwinkligkeit der Normalenvektoren der Ebenen erfüllt ist.

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste

Das Konzept der senkrechten Ebenen

Wenn sich zwei Ebenen schneiden, erhalten wir Diederwinkel $4$. Zwei Winkel sind gleich $\varphi $ und die anderen beiden sind gleich $(180)^0-\varphi $.

Definition 1

Der Winkel zwischen Ebenen ist das Minimum der von diesen Ebenen gebildeten Diederwinkel.

Definition 2

Zwei sich schneidende Ebenen heißen senkrecht, wenn der Winkel zwischen diesen Ebenen $90^\circ$ beträgt (Abb. 1).

Abbildung 1. Senkrechte Ebenen

Zeichen der Rechtwinkligkeit zweier Ebenen

Satz 1

Wenn eine Gerade einer Ebene senkrecht zu einer anderen Ebene steht, dann stehen diese Ebenen senkrecht zueinander.

Nachweisen.

Gegeben seien die Ebenen $\alpha $ und $\beta $, die sich entlang der Geraden $AC$ schneiden. Die Gerade $AB$, die in der $\alpha $-Ebene liegt, sei senkrecht zur $\beta $-Ebene (Abb. 2).

Figur 2.

Da die Gerade $AB$ senkrecht zur Ebene $\beta$ steht, steht sie auch senkrecht zur Geraden $AC$. Zeichnen wir zusätzlich eine Linie $AD$ in der Ebene $\beta$, senkrecht zur Linie $AC$.

Wir finden, dass der Winkel $BAD$ der lineare Winkel des Diederwinkels ist, gleich $90^\circ$. Das heißt, nach Definition 1 beträgt der Winkel zwischen den Ebenen $90^\circ$, was bedeutet, dass diese Ebenen senkrecht zueinander stehen.

Der Satz ist bewiesen.

Aus diesem Satz folgt der folgende Satz.

Satz 2

Wenn eine Ebene senkrecht auf der Schnittlinie zweier anderer Ebenen steht, dann steht sie auch senkrecht auf diesen Ebenen.

Nachweisen.

Gegeben seien zwei Ebenen $\alpha $ und $\beta $, die sich entlang der Geraden $c$ schneiden. Die Ebene $\gamma $ steht senkrecht zur Geraden $c$ (Abb. 3)

Figur 3.

Da die Gerade $c$ zur Ebene $\alpha $ gehört und die Ebene $\gamma $ senkrecht zur Geraden $c$ steht, stehen nach Satz 1 die Ebenen $\alpha $ und $\gamma $ senkrecht zueinander.

Da die Gerade $c$ zur Ebene $\beta $ gehört und die Ebene $\gamma $ senkrecht zur Geraden $c$ steht, stehen nach Satz 1 die Ebenen $\beta $ und $\gamma $ senkrecht.

Der Satz ist bewiesen.

Für jeden dieser Sätze gelten auch die umgekehrten Aussagen.

Beispielprobleme

Beispiel 1

Gegeben sei ein rechteckiges Parallelepiped $ABCDA_1B_1C_1D_1$. Finden Sie alle Paare senkrechter Ebenen (Abb. 5).

Figur 4.

Lösung.

Durch die Definition eines rechteckigen Parallelepipeds und senkrechter Ebenen sehen wir die folgenden acht zueinander senkrechten Ebenenpaare: $(ABB_1)$ und $(ADD_1)$, $(ABB_1)$ und $(A_1B_1C_1)$, $( ABB_1)$ und $(BCC_1) $, $(ABB_1)$ und $(ABC)$, $(DCC_1)$ und $(ADD_1)$, $(DCC_1)$ und $(A_1B_1C_1)$, $(DCC_1) $ und $(BCC_1)$, $(DCC_1)$ und $(ABC)$.

Beispiel 2

Gegeben seien zwei zueinander senkrechte Ebenen. Von einem Punkt auf einer Ebene wird eine Senkrechte auf eine andere Ebene gezogen. Beweisen Sie, dass diese Gerade in der gegebenen Ebene liegt.

Nachweisen.

Gegeben seien senkrechte Ebenen $\alpha $ und $\beta $, die sich entlang der Geraden $c$ schneiden. Vom Punkt $A$ der Ebene $\beta $ wird eine Senkrechte $AC$ zur Ebene $\alpha $ gezogen. Nehmen wir an, dass $AC$ nicht in der $\beta$-Ebene liegt (Abb. 6).

Abbildung 5.

Betrachten Sie das Dreieck $ABC$. Es ist rechteckig mit dem rechten Winkel $ACB$. Daher ist $\angle ABC\ne (90)^0$.

Andererseits ist $\angle ABC$ der lineare Winkel des von diesen Ebenen gebildeten Diederwinkels. Das heißt, der von diesen Ebenen gebildete Diederwinkel beträgt nicht 90 Grad. Wir stellen fest, dass der Winkel zwischen den Ebenen nicht gleich $90^\circ$ ist. Widerspruch. Daher liegt $AC$ in der $\beta$-Ebene.